|
THE AGES OF GAIA: A BIOGRAPHY OF OUR LIVING EARTH |
|
3: Exploring Daisyworld
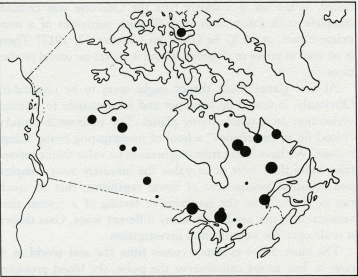
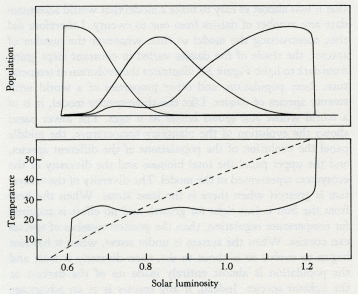
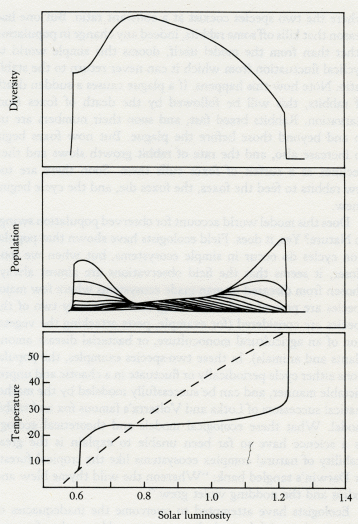
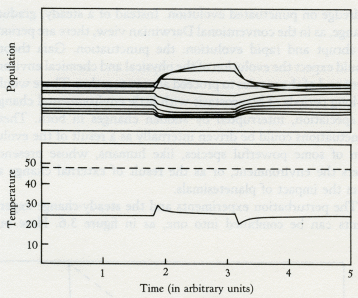
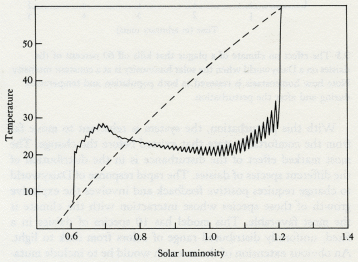
The word theory has the same Greek root as theatre. Both are concerned with putting on a show. A theory in science is no more than what seems to its author a plausible way of dressing up the facts and presenting them to the audience. Like plays, theories are judged according to several different, and barely connected, criteria. Artistic content is important; a theory that is elegant, inspiring, and presented with craftsmanship is universally appreciated. But hard-working scientists like best theories that are full of predictions which can easily be tested. It matters little whether the view of the theorizer is right or wrong: investigation and research are stimulated, new facts discovered, and new theories composed. That it was wrong did little to detract from the theory of continuous creation put forward by the astronomers Hoyle, Bondi, and Gold. It has now been abandoned, but in its day it was a deeply satisfying intellectual concept. The only bad theories are those that cannot be questioned or tested. What use is a theory that the Universe was created, complete with inhabitants, and all with memories of a non-existent past, at 15.37 hr GMT on October 27, 1917? There is no way to prove or disprove it, and it makes no useful predictions. At first glance, Gaia theory might seem to be untestable. Obviously, it would be improper and irresponsible to attempt vivisection on a whole living planet. The nineteenth-century "blood up to the elbows" school of investigating living things is passe. We have learnt from engineers, who value their contraptions more than most of us value the infinitely more complex and beautiful mechanisms of living organisms, that so much can be learnt from the noninvasive testing of a system that vivisection is not needed. In many different ways, Gaia theory is wide open for experimental investigation. The most direct evidence comes from the real world as it now is. Just as we can observe the pulse, the blood pressure, the electrical activity of the heart, and so on without interfering with the normal physiology of a human subject; so we can observe the circulation of air, the oceans, and the rocks. We can measure the seasonal pulsing of the carbon dioxide of the air as the plants breathe it in and the consumers breathe it out. We can follow the course of essential nutrients from the rocks to the ocean to the air and back again, and see how at each step different but interlinked systems are affected. There is also a vast amount of historical evidence preserved in the rocks. During its life span, our planet has suffered the impact of planetesimals. We have been hit by close to thirty small planets, up to 10 miles in diameter and traveling as fast as sixty times the speed of sound. These impacts release about a thousand times as much energy as would be released if all the nuclear powers exploded all the present weapon stocks. Such events do more than make 200-mile craters, they can destroy up to 90 percent of all living organisms from the microscopic to the macroscopic. The impacts make the Earth ring like a bell, and the reverberations of the event resonate, metaphorically, throughout the systems of the Earth for maybe a million years or more. The history of our planet is punctuated by these perturbations; from their record we can learn a great deal about how the system works and the way that homeostasis is fully restored. Should you doubt that the Earth has been so stricken so often, glance at the map of the distribution of craters on the older surface rocks in Canada (figure 3.1). It is like a glance at a region of the Moon's surface. On most of the continental areas and on all the surface of the sea floor, however, the rapidity of the smoothing processes of weathering and sea-floor spreading rapidly remove the evidence of any but the most recent impacts. 3.1 Map of Canada showing large meteor craters. Not all catastrophic events are from external causes; some, such as the appearance of oxygen gas, are generated by inherent internal contradictions within the system and can be likened to such crises in living organisms as puberty, menopause, or the metamorphosis of a pupa to a butterfly. The record of the rocks, though blurred by time and often incomplete, still preserves some evidence of the chemical and physical state of the Earth and of the distribution of the species before and after each of these perturbations. But disentangling the record is rather like trying to find traces of the identity of a terrorist from the rubble of the building his bomb destroyed. The most persuasive criticism of Gaia theory is that planetary homeostasis, by and for living organisms, is impossible because it would require the evolution of communication between the species and a capacity for foresight and planning. The critics who made this challenging, and to me helpful, criticism were not concerned with the practical evidence that the Earth has kept a climate favorable for life in spite of major perturbations, or that the atmosphere is now stable in its composition in spite of the chemical incompatibility of its component gases. They were criticizing from the certainty of their knowledge of biology. No organism as large, and, as they saw her, sentient, could possibly exist. I think this criticism is dogmatic, and, as we saw in the last chapter, it is easy to answer. The simple model Daisyworld illustrated how Gaia might work. It pictured an imaginary world that spun like the Earth as it circled and was warmed by a star that was the identical twin of our own Sun. On this world, the competition for territory between two species of daisies, one dark and one light in color, led to the accurate regulation of planetary temperature close to that comfortable for plants like daisies. No foresight, planning, or purpose was invoked. Daisyworld is a theoretical view of a planet in homeostasis. We can now begin to think of Gaia as a theory, something rather more than the mere "let's suppose" of an hypothesis. There is much more to Daisyworld than just the answer to a criticism. I first made it for that purpose, but as it has developed I have found it to be a source of insight and an answer to questions about theoretical ecology and Darwinism, as well as to questions about Gaia. An important property of the model is its docility and stability in mathematical terms. As I continue to work with these models I find that the number of species that can be accommodated appears to be limited only by the speed and capacity of the computer used and by my patience. Whatever the details, the inclusion of feedback from the environment appears to stabilize the system of differential equations used to model the growth and competition of the species. Most of what follows is the record of my explorations in Daisyworld and an account of the discoveries there. I have assumed that many of my readers are not moved by mathematical expressions, and have therefore not included these. For those who regard any theory not expressed in the pure language of mathematics as at best inadequate, Andrew Watson and I have described the mathematics of Daisyworld in our paper in Tellus. In no way is the stability of Daisyworld dependent upon an idiosyncratic choice of initial values, or rate constants, and as we shall see in later chapters the model is general in its application. It may still be that some of the diagrams used to illustrate the geophysiology of the model planet are difficult to follow for readers unfamiliar with this form of graphic explanation. For you, I have written this book so that this chapter can be skipped without much loss, provided that you are already convinced that Gaia theory gives a fair representation of the Earth. But I ask my critics to read on, for here I shall try to answer in detail the objections they have raised. The reaction of scientists to the Daisyworld model was revealing. Meteorologists and climatologists were the most interested; geologists and geochemists next. With rare exceptions, biologists either ignored the models or remained as skeptical as ever. A persistent criticism from biologists was that, in a real world, daisies would have to use some of their energy to make pigment and therefore would be at a disadvantage compared with unpigmented gray daisies. In such a world no temperature regulation would take place. As they put it, "the gray daisies would cheat." Stimulated by their criticism I made a model with three species of daisies. All that the new model required was another set of equations to describe the temperature and growth of the gray daisy species. It was a matter of introducing sober-suited middle-management daisies to a world of colorful eccentrics. I charged the dark and light daisies a 1 percent growth-rate tax to make pigments. I am pleased to report that the biologists' cynical view of the world is not supported by this new model, as you can see from the results in figure 3.2. Again, the solar luminosity increases from 60 to 140 percent of that of our own Sun. The populations of the daisies are on the upper panel, with dark on the left, gray in the middle, and light on the right. The fact that gray daisies use no energy to make pigment avails them of nothing when their world is too hot or too cold for them to grow. But dark daisies can flourish in the cold, and white ones in the hot. Gray daisies do best when the climate is temperate and when regulation is not needed. In other words, the different species grow when they and their environment are fit for one another. Solar luminosity 3.2 The evolution of the climate on a three-species Daisyworld with dark, gray, and light daisies present. By comparison, the dashed line in the lower panel represents the temperature evolution in the absence of life. It would have been sufficient as an answer to the critics merely to have added gray daisies, but having started, I found that it was almost as easy to make a model that would accommodate any number of daisies from one to twenty. I therefore did this, constructing the model so that, whatever the number of species, the shade of the daisies varied in constant steps going from dark to light. Figure 3.3 illustrates the evolution of temperature, daisy population, and other properties of a world with twenty species of daisies. Like the three-species model, it is of a world whose star grows hotter as it ages. The lower panel shows the evolution of the planetary temperature, the middle panel the evolution of the populations of the different species, and the upper panel the total biomass and the diversity of the ecosystem represented in the model. The diversity of the ecosystem is greatest when there is the least stress. When the heat from the Sun is just right for growth and no effort is required for temperature regulation, then the greatest number of species can coexist. When the system is under stress, when it has just begun to evolve or is about to die, then diversity is least and the population is almost entirely made up of the darkest or the lightest species. Indeed, if any species is at an advantage at such times, it is the darkest or the lightest, not the gray. But there is much more to this new model than an answer to the criticisms of skeptical biologists. When I made it I was ignorant of theoretical ecology, that branch of mathematical biology that is concerned with interactions among the species of an ecosystem. As we shall see, Daisyworlds provide an escape for a science that has been trapped for years by the limitations of its theories. In the 1920s, the mathematical biologists Lotka and Volterra introduced their famous model of the competition between rabbits and foxes. Like Daisyworld it was a simple model, but it differed in that the environment was taken as infinite and neutral. The growth of the populations of rabbits or foxes did not affect the environment, and no environmental changes were allowed to affect the rabbit and fox populations. The two equations for this world can be expressed in words as follows: Foxes increase as the numbers of rabbits grow, but rabbits decline as the foxes increase. In this relationship, there is one stable point where the two species coexist at a constant ratio. But one bad season that kills off some rabbits, indeed any change in population other than from the model itself, dooms this simple world to cyclical fluctuation from which it can never return to the stable ratio. Note how this happens. If a plague causes a sudden death of rabbits, this will be followed by the death of foxes from starvation. Rabbits breed fast, and soon their numbers are up to and beyond those before the plague. But now foxes begin to increase also, and the rate of rabbit growth slows and then declines as a surfeit of foxes culls them. Soon there are too few rabbits to feed the foxes, the foxes die, and the cycle begins anew. Solar luminosity 3.3 The evolution of the climate on a 20-species Daisyworld. The lower panel illustrates planetary temperature -- the dashed curve with no life present, and the solid line with daisies. The middle panel shows the populations of the 20 different colored daisies, with the darkest appearing first (left) and the lightest last (right). The upper panel illustrates diversity, seen to be maximum when the system temperature is closest to optimum. Does this model world account for observed population swings in Nature? Yes, it does. Field ecologists have shown that population cycles do occur in simple ecosystems, but when we look closer, it seems that the field observations are almost always chosen from diseased or man-made ecosystems where few major species are present and interacting, and when only two of the species are considered (for example, pests attacking the vegetation of an agricultural monoculture, or bacterial disease among plants and animals). In these two-species examples, the populations either cycle periodically or fluctuate in a chaotic and unpredictable manner, and can be successfully modeled by the mathematical successors of Lotka and Volterra's famous fox and rabbit model. What these ecological models and theoretical ecology as a science have so far been unable to explain is the great stability of natural complex ecosystems like the tropical forests or Darwin's tangled bank: "Whereon the wild thyme blew and oxlips and the nodding violet grew." Ecologists have attempted to overcome the inadequacies of their simple models by including a structured hierarchy of species that are referred to as "food webs." In such a hierarchy there is a pyramid that is surmounted by the top predator, such as a lion, with the smallest numbers. The numbers increase as you go down each "trophic" level, until at the base of the pyramid are the most numerous primary producers, the plants, that provide food for the whole system. In spite of years of effort and computer time, the ecologists have made no real progress towards modeling a complex natural ecosystem such as a tropical rain forest or the three-dimensional ecosystem of the ocean. No models drawn from theoretical ecology can account in mathematical terms for the manifest stability of these vast natural systems. Indeed, a distinguished ecologist, Robert May, in his book Theoretical Ecology, writes in a chapter entitled "Patterns in Multispecies Ecosystems":
May goes on to write:
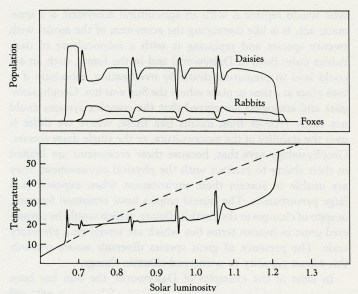
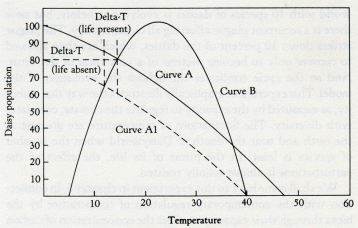
This disclaimer recognizes the stability of complex ecosystems in the real world; but the impression remains that diversity is, in general, a disadvantage and that Nature, by disregarding the elegant mathematics of theoretical biology, has somehow cheated. Obviously, had I known of this work, I would never have attempted anything so foolish as a model with twenty daisies. Fortunately for me I was brought up in that school of science that believes in reading the books after rather than before an experiment. What is it, then, that confers the great stability and freedom from cyclical and chaotic behavior on the Daisy' world models? The answer is that in Daisyworld the species can never grow uncontrollably; if they do, the environment becomes unfavorable and growth is curtailed. Similarly, while daisies live, the physical environment cannot move to unfavorable states; the responsive growth of the appropriately colored daisy prevents it. It is the close coupling of the relationships which constrain both daisy growth and planetary temperature that makes the model behave. Perhaps it is a metaphor for our own experience that the family and society do better when firm, but justly applied, rules exist than they do with unrestricted freedom. Curious to see if this explanation was correct, I made an additional Daisyworld. In this one, the daisies were grazed by rabbits and the rabbits in turn eaten by foxes -- a combination of Lotka and Volterra's model with Daisyworld. To test the stability of this more complex model, I subjected it to periodic catastrophes; on four occasions during the evolution of the model 30 percent of the daisy population was destroyed suddenly as by a plague, and the system then allowed to recover (see figure 3.4). Remarkably, neither the addition of herbivores nor plagues seriously affects the capacity of the daisies to regulate climate. During the normal course of evolution all populations are stable and recover promptly from the perturbations of the plagues. Eventually, the system can no longer cope with the ever-increasing solar output and it fails. As one might expect, the nearer to failure the greater the effect of the perturbations. The difference between the geophysiological and the ecological view is in the interpretation of perturbation. The geophysiologists see temperature, rainfall, the supply of nutrients, and so on as variables that might be perturbed. In their view the Gaian system evolved with its physical and chemical environment and is well able to resist changes of this kind. Forests of the humid tropics are normally well watered and shaded by their canopy of clouds; during their existence they are never subjected to prolonged drought as in a desert region. Theoretical ecologists, on the other hand, ignore the physical and chemical environment; to them the environment means the collection of species themselves and a niche is some piece of territory negotiated among the species, rather as one might regard the environment of Switzerland as comprising the people of Italy, France, and Germany. In such a view, perturbations are competition or wars. Solar luminosity 3.4 Daisyworld with rabbits and faxes, perturbed by four plagues that killed 30 percent of the daises. The invasion of a tropical forest by humans with chain saws who would replace it with an agricultural ecosystem is a traumatic act. It is like destroying the ecosystem of the model with twenty species and replacing it with a monoculture of dark daisies only. Both in Daisyworld and in the forest, such an act could lead to premature death by overheating, especially if it took place at a time or place where the Sun was hot. Geophysiologists and ecologists are agreed that the complex systems could not easily recover from insults like these; where we differ is over the stability of the monoculture, or the single daisy species. Geophysiology says that, because these ecosystems are limited in their ability to interact with the physical environment, they are unable to sustain their environment when exposed to a large perturbation. The humid tropics have remained forested, in spite of changes in the Earth's climate, which would be considered great in human terms but which are trivial on a planetary scale. The presence of great species diversity assists towards this robust capacity to withstand climatic change. In most of the examples of Daisyworld, the Sun has been shown as steadily increasing its output of heat; an external perturbation that relentlessly increases in intensity until life can no longer continue. An alternative way of illustrating the stability of Daisyworld is to allow life to go on normally at a constant intensity of sunlight and then suddenly perturb the world by a change in climate or by some catastrophe such as a plague or planetesimal impact. Figure 3.5 shows a Daisyworld with 10 species of colored daisies whose stable existence is suddenly disturbed by a plague that kills 60 percent of the daisies, regardless of their color. In the lower panel, the dashed line represents the planetary temperature with no daisies present; at 40°C it is at the limit for life. The solid line illustrates the climate with daisies present before, during, and after the perturbation. The temperature stays in the mid-twenties, except when the plague first hits the daisy populations. When the perturbation is relaxed the system rapidly restores the status quo. The upper panel illustrates the variation in the distribution of species before, during, and after the catastrophe. Time (in arbitrary units) 3.5 The effect on climate of a plague that kills off 60 percent of the daisies on a Daisyworld when the solar luminosity is at a constant intensity. Note how homeostasis is restored in both population and temperature during and after the perturbation. With this perturbation, the system is reluctant to move far from the comfortable state that existed before the change. The most marked effect of the disturbance is in the distribution of the different species of daisies. The rapid response of Daisyworld to change requires positive feedback and involves the explosive growth of those species whose interaction with the climate is the most favorable. This model has 10 species of daisies in a fixed, uniformly distributed range of colors from dark to light. An obvious extension of the research would be to include mutations and the possibility of evolutionary changes in the species. The abrupt change in the distribution of species at the perturbation event and again at its termination indicates the intensity of the selection pressure at these times. The experiment is much in accord with the observations of Stephen Jay Gould and Niles Eldredge on punctuated evolution. Instead of a steady, gradual change, as in the conventional Darwinian view, there are periods of abrupt and rapid evolution: the punctuation. Gaia theory would expect the evolution of the physical and chemical environment and of the species to proceed always together. There would be long periods of homeostasis with little environmental change or speciation, interrupted by sudden changes in both. These punctuations could be driven internally as a result of the evolution of some powerful species, like humans, whose presence alters the environment, or as the result of external change as from the impact of planetesimals. The perturbation experiments and the steady-change experiments can be combined into one, as in figure 3.6. Here our world with 10 species of daisies is evolving as before, but now there is a recurrent plague affecting all colors equally. The plague strikes down 10 percent of the daisies, which are then allowed to recover only to become victims of a new form of the virus. And so the cycle continues throughout the evolution of the model. This experiment graphically illustrates the way that stability, as measured by the capacity to regulate the climate, correlates with diversity. The fluctuations of temperature are greatest at the birth and near the death of Daisyworld when the number of species is least. In the prime of its life, the effect of the perturbations is almost wholly resisted. Solar luminosity 3.6 The effect of a periodic plague of constant intensity on the ability of the daisies to control the climate. Note how the perturbation of the plague is amplified at the times of maximum stress near the beginning and the end of daisy life. The increasing amplitude of the oscillations in the latter part of the curve is reminiscent of the evolution of the present series of glacials and interglacials. We shall come back to this experiment in chapter 6, in connection with the contemporary regulation of temperature by the biota through their capacity to affect the concentration of carbon dioxide in the air. This particular climate control system is nearing the end of its capacity to work and it can be argued that the recent oscillation of climate between ice ages and interglacials is like that near the end of Daisyworld in figure 3.6. The relatively minor perturbations of the Earth's orbital wobble that cause small variations in the amount of heat received from the Sun are amplified by the instability of a moribund system. These arguments do not necessarily apply to glaciations in the more remote past, which are likely to have had different causes. The Daisyworld models that I have just described are complete but are expressed in ordinary English. Many scientists find such an expression of a theory unsatisfying and prefer the "rigor" of formal mathematical expression. For their benefit, the essence of the Daisyworld model is expressed in the simple diagram, figure 3.7, that my friend and colleague, Andrew Watson, devised. This model is based on a Daisyworld where there are only white daisies present. Because they are lighter in color than the soil in which they grow, they tend to increase the albedo of their locality, which, as a consequence, is cooler than a comparable area of bare ground. Where the daisies cover a substantial proportion of the planetary surface they will influence the mean surface temperature of the planet. The relationship between the area covered by white daisies and the mean surface temperature of the planet is illustrated as curve A. The parallel dashed line (A1) shows how the relationship might be shifted if there were a change in some external variable that influenced the planetary temperature -- for instance, if the star that warmed Daisyworld decreased its output of radiant heat. Temperature 3.7 Regulation by white daisies. The helmet-shaped curve (B) depicts the response of the daisies to temperature, and curves A and A1 are the response of planetary temperature to the area covered by daisies. Curve A1 is for a lower heat input from the star. In the absence of daisies, the change of planetary temperature (Delta-7) would be nearly 15°C whereas in their presence it is only about 3°C. Like most plant life, daisies grow best over a restricted range of temperatures. The growth peaks near 20°C and falls to zero below 5°C and above 40°C. The relationship between planetary surface temperature and the steady-state population of daisies will be as in curve B, the curve shaped like a helmet. Curves A and B relate the planetary temperature to the population of Daisyworld at steady state; and the steady state of the whole system is specified by the point of intersection of these two curves. In the example, it can be seen that there are two possible steady-state solutions. It turns out that the stable solution is at the intersection where the rates of change of population with temperature are in opposite directions. In mathematical terms, where the derivatives of the two curves have opposite signs. The other intersection does not give a stable solution. If Daisyworld is started at some arbitrary but tolerable temperature it will move to the upper intersection point and settle there. What happens to this stable state when some change takes place in the external environment? Suppose, for example, that the star warms up as our Sun is said to be doing. If the daisy population were artificially held constant, the planetary temperature will simply follow the change of heat output of the star; there will be a much larger change of temperature than if the daisies were allowed to grow to their new natural steady state, where they would oppose the effect of a change of stellar output. Very few assumptions are made in this model. It is not necessary to invoke foresight or planning by the daisies. It is merely assumed that the growth of daisies can affect planetary temperature, and vice versa. Note that the mechanism works equally well whatever the direction of the effects. Black daisies would have done as well. All that is required is that the albedo when the daisies are present be different from that of the bare ground. The assumption that the growth of daisies is restricted to a narrow range of temperatures is crucial to the working of the mechanism, but all mainstream life is observed to be limited within this same narrow range. The peaked growth curve (B) is common to other variables besides temperature, for example pH (it can be too acid or too alkaline: neutrality is preferred). Similar restrictions apply to most nutrients; too much is poisonous, too little causes starvation. The choice of a parabolic relationship for the response of daisy growth to temperature is arbitrary, and some people suggested that in real life the relationship takes on different or more complex forms. To test this objection, the Daisyworld model was run with different relationships between growth and temperature. These all retained the 5 to 40°C limit but ranged in shape from rectangular (a constant growth at all temperatures) to triangular (a linear increase up to a maximum, and then a linear decrease back again). Semicircular and rhombic relationships were also tried. The only limitation observed was that the models became unstable when a horizontal section was present in the relationship. Look back at figure 3.7 and imagine the helmet-shaped curve is replaced by one shaped as a top hat. The horizontal section, the top of the hat, would imply constant growth at any temperature within the 5 to 40°C range; consequently no regulation of temperature could take place. Such models are very similar to the simple competitive models of population biology where the environment is ignored and which are notoriously unstable. So long as the rate of growth of daisies varies with their temperature up to a maximum and then declines, even the gentle curvature of the top of a semicircle provides a working model. In Nature, the shape of the relationship linking growth with some environmental variable frequently comes from the combination of a logarithmic rise overtaken by a logarithmic decay. In chapters 5 and 6 this relationship forms part of the model for the regulation of atmospheric oxygen. As oxygen increases in abundance the growth of consumers increases, but oxygen in excess is poisonous. Too little oxygen and too much both are bad; there is a desirable sufficiency. Daisyworld differs profoundly from previous attempts to model the species or the Earth. It is a model more like those of control theory, or cybernetics, as it is otherwise called. Such models are concerned with self-regulating systems; engineers and physiologists use them to design automatic pilots for aircraft or to understand the regulation of breathing in animals, and they know that the parts of the system must be closely coupled if it is to work. In their parlance, Daisyworld is a closed-loop model. Devices that are not self-regulating are often unstable. Engineers refer to them as "open-loop"; the loops are the feedback links between the parts of the system. Daisyworld is not identical in form to an engineered device; a key difference is the absence, in Daisyworld, and perhaps in Gaia also, of "set points." In manufactured systems, the user sets the temperature, the speed, the pressure, or any other variable. The value chosen is the set point, and the goal of the system is to keep that value, however the external environment changes. Daisyworld does not have any clearly established goal like a set point; it just settles down, like a cat, to a comfortable position and resists attempts to dislodge it. Because of the tribalism that isolates the denizens of the scientific disciplines, biologists who made models of the competitive growth of species chose to ignore the physical and chemical environment. Geochemists who made models of the cycles of the elements, and geophysicists who modeled the climate, chose to ignore the dynamic interactions of the species. As a result, their models, no matter how detailed, are incomplete. It is as if, in figure 3.7, the biology of the relationship between daisy population and temperature was considered without reference to the complementary geophysics of the relationship between temperature and daisy population. An engineer or physiologist would instantly recognize that such an approach was "open-loop," and consequently of little value except as an example of an extreme or pathological condition. There is also something pathological about the hubris of those scientists who boast of their special knowledge and of their disdain for that of other scientific disciplines. Sixty years ago that wise and generous-minded American theoretical biologist, Alfred Lotka, described the model of the competition of rabbits and foxes in The Elements of Physical Biology. It has been the inspiration of countless researchers in population biology ever since, yet none can have heeded his warning on page 16:
For three generations since, theoretical ecologists have modeled the evolution of ecosystems while ignoring the physical environment; and three generations of biogeochemists have modeled the cycles of the elements without ever including the organisms as part of a dynamic and responsive system. In Alfred Lotka's time the resolution of systems of nonlinear differential equations, even for a simple model like Daisyworld, was a daunting task. With the ready availability of computers there is now no need to continue with models constrained by the narrow limits of a single scientific discipline. Lotka's insight, that modeling would be simpler with the whole system than with any part of it, is amply confirmed by modern mathematics. Systems of equations of the type describing model systems in theoretical ecology and biogeochemistry are notorious for their chaotic behavior, so much so that they now seem more interesting as playthings, or a new form of graphic illustration. The mathematics of natural phenomena, when constrained within a single discipline, can become so intricate and complex that world after world of colorful abstraction opens at every new level investigated. It is small wonder that practitioners of the various disciplines imagine that in these imaginary worlds they see glimpses of real world whereas in fact they are lost in the fractal dimensional world of a Mandelbrot set that goes on forever at every level from minus to plus infinity. The delusion is encouraged by professional mathematicians who find similarities between their mathematical theories and the pathologies of the real world, and the numerous modern mathematical scientists whose contemplation of the demons of hyper-space -- the "strange attractors" of chaos -- is much more beguiling than the dull old real world of Nature. Daisyworld provides a plausible explanation of how Gaia works and why foresight and planning are not required for planetary regulation. But what evidence is there of practical mechanisms? What predictions from Gaia theory have been confirmed? Is it testable? The first test was the Viking mission to Mars. That expedition confirmed the prediction, from atmospheric analyses by infrared astronomy, that Mars was lifeless. Michael Whitfield, Andrew Watson, and I predicted that the long-term regulation of carbon dioxide and climate is by the biological control of rock weathering. These and other tests are described in the three chapters that follow. It matters little whether Gaia theory is right or wrong; already it is providing a new and more productive view of the Earth and the other planets. Gaia theory provokes a view of the Earth where 1. Life is a planetary-scale phenomenon. On this scale it is near immortal and has no need to reproduce. 2. There can be no partial occupation of a planet by living organisms. It would be as impermanent as half an animal. The presence of sufficient living organisms on a planet is needed for the regulation of the environment. Where there is incomplete occupation, the ineluctable forces of physical and chemical evolution would soon render it uninhabitable. 3. Our interpretation of Darwin's great vision is altered. Gaia draws attention to the fallibility of the concept of adaptation. It is no longer sufficient to say that "organisms better adapted than others are more likely to leave offspring." It is necessary to add that the growth of an organism affects its physical and chemical environment; the evolution of the species and the evolution of the rocks, therefore, are tightly coupled as a single, indivisible process. 4. Theoretical ecology is enlarged. By taking the species and their physical environment together as a single system, we can, for the first time, build ecological models that are mathematically stable and yet include large numbers of competing species. In these models increased diversity among the species leads to better regulation. We have at last a reason for our instinctive anger over the heedless deletion of species; an answer to those who say it is mere sentimentality. No longer do we have to justify the preservation of the rich variety of species in natural ecosystems, like those of the humid tropical forests, on the feeble humanist grounds that they might, for example, carry plants with drugs that could cure human disease. Gaia theory makes us wonder if they offer much more than this. Through their capacity to evaporate vast volumes of water vapor through the surface of their leaves, trees serve to keep the ecosystems of the humid tropics and the planet cool by providing a sunshade of white reflecting clouds. Their replacement by cropland could precipitate a regional disaster with global consequences.
|